Плотность тока

Электрические заряды, находящиеся в движении, формируют электрический ток. Если формально, электрическим током называется всякое упорядоченное движение электрических зарядов в пространстве. Одной из характеристик электрического тока является сила тока. Силой тока сквозь некоторую поверхность \(S\) называется скалярная величина \(I\), равная первой производной по времени от заряда \(Q\), проходящего через эту поверхность:

\[ I=\frac{dQ}{dt} \]

Единица измерения силы тока - Ампер. Один Ампер равен количеству заряда (Кулон, Кл), протекающему через заданную поверхность за единицу времени (секунда, с).

В теории поля обычно интерес представляют процессы, протекающие в точке, а не в пределах некоторой большой области пространства. В этом случае удобно использовать другую, векторную характеристику электрического тока - плотность электрического тока. Вектор плотности электрического тока \(\vec{J}\) характеризует распределение электрического тока по сечению \(S\). Единицы измерения - Ампер/метр\(^2\).

Приращение силы тока \(\Delta I\), пересекающего бесконечно малый элемент поверхности \(\Delta S\), нормальный к плотности тока, равно:

\[ \Delta I=J_N \Delta S \]

Если вектор плотности тока ориентирован под углом к элементу поверхности, то силу тока можно найти скалярно перемножив векторы \(\vec{J}\) и \(\vec{S}\):

\[ \Delta I=\vec{J}_N \cdot \Delta \vec{S} \]

Напомним, что скалярное произведение равно произведению модулей двух векторов и косинусу угла между этими векторами. Таким образом, если между векторами \(\vec{J}\) и \(\vec{S}\) угол \(90^\circ\), то ток через такую поверхность равен нулю.

Вектор \(\vec{S}\) направлен в ту же сторону, что и нормаль к той плоскости, которая является касательной к поверхности в рассматриваемой точке. Конечно, существуют две такие нормали. Мы будем рассматривать внешнюю нормаль, если не указано иное.

Полный ток будет равен интегралу вектора \(\vec{J}\) по поверхности \(S\):

\[ I=\int_{S} \vec{J} \cdot \partial\vec{S} \]

Плотность тока в некоторой точке связана со скоростью зарядов. Рассмотрим область пространства, равномерно заполненную зарядами. Для простоты будем рассматривать электроны. Заряд электрона обозначим \(q_e\). Плотность электронов в единичном объеме равна \(N_e\). Выделим в данной области пространства куб объемом \(\Delta S \Delta L\) (рис. 1 слева). Общий заряд электронов, которые находятся в этом кубе, можно вычислить, умножив плотность электронов на их заряд и на объем выбранного куба - \(\Delta Q=q_e N_e \Delta S \Delta L\).

alt text

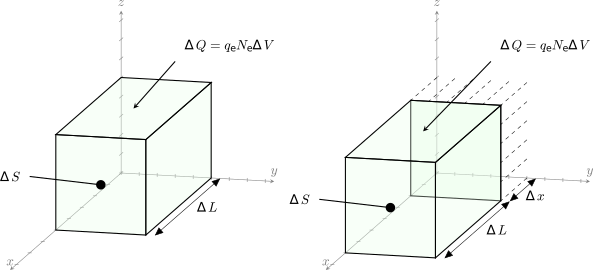
Рис. 1. Заряд \(\Delta Q= q_e N_e \Delta S \Delta L\), который перемещается на расстояние \(\Delta x\) за время \(\Delta t\) порождает ток с плотностью \(\Delta t\) \(J_x = q_e N_e \upsilon_x\).

Пусть выбранный куб с электронами существует в свободном пространстве. Рассмотрим их перемещение вдоль координаты \(x\). За время \(\Delta t\) общий заряд \(\Delta Q\) переместится на расстояние \(\Delta x\), как показано на рисунке 1 справа. Таким образом, заряд \(\Delta Q=q_e N_e \Delta S \Delta x\) переместился через “контрольную” плоскость, которая ориентирована перпендикулярно направлению движения, за время \(\Delta t\). Тогда сила тока будет равна:

\[ \Delta I=\frac{\Delta Q}{\Delta t}=N_e q_e \Delta S \frac{\Delta x}{\Delta t} \]

Устремим \(\Delta t\) в знаменателе к нулю и по определению производной получим:

\[ \Delta I=N_e q_e \Delta S \upsilon_x \]

,где \(\upsilon_x\) — это \(x\)-компонента скорости \(\vec{\upsilon}\) по определению. Тогда из записанной выше связи между приращением силы тока и плотностью тока получается выражение для \(x\)-компоненты плотности тока:

\[ J_x=N_e q_e \upsilon_x \]

И общее выражение для плотности тока:

\[ \vec{J}=N_e q_e \vec{\upsilon} \]